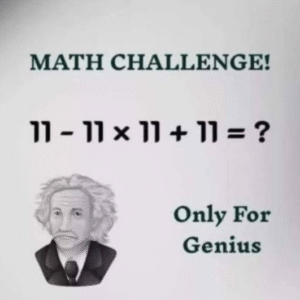🧩 The Equation That Tricks the Eye

Equations are often thought of as tools of precision—symbols and numbers designed to describe the world with absolute clarity. Yet, surprisingly, math can also be used to trick the eye and create illusions. Certain equations, patterns, and visual formulas exploit the way our brains interpret geometry, light, and proportion. Instead of showing us reality, they show us how easily we can be misled by it.

In this article, we will journey into the fascinating world where mathematics and psychology meet art, uncovering how equations create optical illusions, why our eyes believe them, and what they reveal about perception itself.

The Science of Seeing: Why Illusions Work

To understand how an equation can trick the eye, we must first understand how vision works. When light enters our eyes, it strikes the retina, where photoreceptor cells send electrical signals to the brain. The brain then constructs an image from these signals.

But this process is not flawless—it’s based on shortcuts. Our brains rely on context, patterns, and assumptions to interpret the flood of sensory data. These shortcuts usually help us survive in a chaotic world, but they also make us vulnerable to illusion.

For example:

• We assume parallel lines converge in the distance (perspective).

• We assume shadows mean depth (light interpretation).

• We assume size based on surroundings (relative perception).

When equations mimic these assumptions, they create pictures that feel real but are mathematically false.

Equations That Trick the Eye

1. The Müller-Lyer Illusion (Lines and Arrows)

The Müller-Lyer illusion is a famous example of geometry tricking perception.

Two lines of equal length are drawn, but one has outward-pointing arrowheads (> <) and the other inward (< >). Almost everyone perceives the line with inward arrows as longer—even though they are identical.

Mathematically, both lines measure the same length. But the “arrow equation” changes our perception. The brain interprets the angles as depth cues, stretching one line mentally into a “longer corridor.”

2. The Sine Wave Grating

Equations involving sine and cosine waves are often used in visual illusions. A simple sin(x) pattern can generate stripes that appear to bend or shimmer depending on contrast and spacing.

Neuroscientists often test vision using these gratings because our visual cortex is highly sensitive to repetitive wave patterns. The math of sine and cosine is precise, but our brain interprets it as motion or distortion.

3. The Impossible Triangle (Penrose Triangle)

The Penrose Triangle is one of the most famous “impossible objects.” On paper, its three sides seem to form a continuous triangular beam. In reality, no 3D shape could exist like this.

Mathematically, the triangle works by aligning 2D projections of 3D objects. The equations of perspective geometry allow the drawing to appear consistent, even though it violates physical space.

This trick shows how our brains trust linear perspective equations more than real spatial reasoning.

4. Checker Shadow Illusion

In Edward Adelson’s illusion, a checkerboard has alternating light and dark squares. A shadow falls across the board, making some dark squares appear light and some light squares appear dark.

Mathematically, the pixel values of the two compared squares are identical—but the brain, applying its “shadow correction algorithm,” insists they are different.

This is where math and perception diverge: the equation of light intensity is simple, but the brain overlays assumptions about lighting, creating the illusion.

Fractals: Equations That Trick Scale

Fractals are equations that repeat infinitely, creating patterns that look natural and organic. The Mandelbrot set, defined by the equation:

z → z² + c

produces swirling, self-replicating shapes. Zoom into any part of the set, and you’ll find structures resembling the whole.

To the eye, fractals look like forests, rivers, or galaxies. The trick lies in scale invariance: our brains are used to objects changing with distance, but fractals stay complex no matter how close we look. This creates an eerie, almost hypnotic visual effect—mathematics mimicking nature too perfectly.

Motion Illusions: Static Equations That Move

Some illusions even make static images appear to move. This usually happens when repeating equations of color, shape, and spacing overstimulate the visual system.

• Peripheral drift illusions: Circular patterns, designed using radial sine waves, create a sensation of rotation when viewed indirectly.

• Ouchi illusion: A checkerboard pattern offset by a geometric shape appears to float or shift when you move your eyes.

Here, equations exploit tiny delays in how our retina processes contrast, producing phantom motion.

Art Meets Math: The Equation as Illusionist

Artists throughout history have unknowingly harnessed mathematical illusions:

• The Renaissance masters perfected perspective equations to create depth on flat canvases.

• Op Art (Optical Art), pioneered by artists like Bridget Riley, deliberately used geometric formulas to create vibrating, shifting images.

• Digital artists now use algorithms and fractal equations to design illusions that can’t be drawn by hand.

These creations blur the line between science and art, showing that equations are not just about numbers—they are about perception.

Why Our Brains Fall for It

So why do we fall for these tricks again and again? Cognitive science points to a few reasons:

1. Efficiency over accuracy

   • The brain processes millions of visual signals per second. To save energy, it uses shortcuts, even if they are sometimes wrong.

2. Context dominance

   • We interpret objects relative to their surroundings. A square in shadow looks lighter or darker depending on its neighbors.

3. Evolutionary bias

   • Our ancestors survived by interpreting depth, light, and movement quickly. Illusions exploit those survival shortcuts.

4. Math mirrors reality

   • Equations like sine waves, fractals, and linear perspective resemble patterns in nature. Our brains trust them automatically.

Lessons from Illusions

Optical illusions aren’t just parlor tricks—they reveal deep truths about human perception. Studying them has practical value:

• Neuroscience: Understanding how the brain misinterprets signals helps scientists treat visual disorders.

• Design: Architects and advertisers use illusions to influence how spaces and products are perceived.

• AI Vision: Training artificial intelligence to recognize illusions helps refine how machines “see.”

Equations that trick the eye show us where our perception diverges from reality—and why awareness of these gaps matters.

Conclusion: Numbers, Perception, and Wonder

The phrase “the equation that tricks the eye” captures something profound: math, the language of clarity, can also be the language of deception. Not deception in a malicious sense, but in the playful, mysterious way our brains can be led astray.

From the Müller-Lyer illusion’s simple arrows to the infinite spirals of fractals, equations remind us that what we see is not always what is. Our vision is less a camera than a storyteller—one that bends reality to fit its expectations.

The beauty of these illusions lies not in fooling us, but in teaching us humility. They remind us that the world is richer, stranger, and more complex than our senses alone can grasp. And sometimes, the best way to see truth is to be tricked by it first.